To Infinity and Beyond!
Infinity is one of those concepts that sounds simple but really isn’t. It’s a concept that simultaneously fascinates us, yet trips over even the most studious mathematician.
Briefly put, something is infinite if I can always find one more thing. For example, if I were to look at, for example, all the cars in the United States, I could – theoretically – just go and identify all the cars. After each, I’ll ask, “Is there another?” and eventually, there won’t be any more. The set of all cars in America is finite.
When you think about most physical sets of things you can count, you’ll find they’re finite. Even the number of particles in the known universe (estimated to be around around \(10^{80}\)) is – again, very theoretically – finite. You can identify all of them, if you had a lot of time.
So what’s infinite? Well, since we’re looking at mathematics, we can just define things. Let’s construct an infinite thing.
My first thing that is part of my set of infinite things I’ll just call \(Z\). Now I have a box containing \(Z\). Excellent!
Okay, I need to find one more thing. Again, since mathematicians just invent stuff, we’ll call the next thing \(SZ\), where \(S\) stands for successor. Now if I want the next thing, I’ll just call that \(SSZ\). Great. I have a set of infinite things. Conceptually, you can give me any thing in this notation and if you ask me for one more, I add an \(S\) and give it back. Even if the number of \(S\)’s conceptually exceeds the number of known particles in the universe, I can still describe the next number to you. It’s just an \(S\) and then \(10^{80}\) more S’s and then a \(Z\).
That seems pretty infinite to me right? I mean, we just go on forever. There will never be a thing in this set that I cannot stick another \(S\) in front of.
Congratulations! We have discovered our first infinite thing. And – conveniently – this thing happens to be the natural numbers1.
Arithmetic: the study of infinity
Many people mistakenly believe arithmetic to be about the manipulation of numeric digits. That’s true at one level, but if we take a step back, we can also frame it as something more profound. Arithmetic is, fundamentally, the study of infinity. The natural numbers are the first thing that most children encounter that is truly, tangibly infinite. Literally nothing within our universe is infinite. Everything has bounds. Infinity exists only as an idea, and the numbers are almost always the first infinite idea any child will have. Many children have bothered their fathers and mothers with incessant questions as to “What’s the largest number?”. Such questions are the foundation of future mathematical thinking.
Natural numbers are usually introduced along with operations. One of the most fundamental operations kids learn is the addition of \(0\), which we all know is as follows:
\[x + 0 = x.\]
Addition is a binary operation. It takes two numbers and produces another. In this instance, the equation tells us that no matter what we add to 0, we get the thing itself. Always. No exceptions. Again, a study of infinity, because it holds for all numbers.
There is no other number for which adding it to another will always yield the other. Zero is unique, We call it the identity of addition.
Another nice property of a binary operation is the existence of inverses. Consider just the natural numbers (0, 1, 2, …). Is there any answer to the following?
\[2 + \square = 0\]
The answer is no. In the natural numbers, addition always yields something greater.
Luckily, again, as mathematicians, we can just make stuff up, so we can complete the natural numbers by including amongst them a set of numbers noted \(-x\) for any natural number \(x\) that, when added to \(x\), yields zero.
Thus, we can answer what number should be filled in \(2 + \square = 0\) as \(-2\), which is a concept I just made up, but you probably already heard about it.
Anyway, the natural numbers along with their additive inverses is called the integers (also referred to as \(\mathbb{Z}\)).
United we stand, divided we fall
The other basic arithmetic operation is multiplication, which is just repeated addition. Like addition, multiplication also has an identity. You can prove using logic that this number is exactly the number after zero, \(SZ\) or \(1\). Again, going back to infinity, for every single infinite number of \(x\) you can say
\[x \times 1 = x\]
That is to say, one is the identity of multiplication.
Again, we ask, do the integers contain the inverses of multiplication? That is, is there a number such that
\[2 \times \square = 1?\]
Here, two is chosen arbitrarily, while one is the identity for multiplication.
Of course the answer is no, while we now have numbers (the negative ones) that, when multiplied by a positive, will produce a number less than that number, they’ll never hit one. The integers are incomplete in relation to multiplication.
Again, we can just make stuff up, so we can go ahead and define new numbers labeled \(\frac{1}{x}\) for all \(x\), such that
\[x \times \frac{1}{x} = 1\]
Notice, however, that unlike the integers, where we only needed to add these new \(-x\)s, here, we actually have to add a whole lot more. Let’s examine.
Suppose I do \(2 + x\), where \(x\) is a negative number. What number do I get? Well it’s just one of the natural numbers \(0, 1, 2\) or it’s a negative number.
However, for the multiplicative inverses \(\frac{1}{x}\), this does not hold.
For \(2 \times \frac{1}{x}\), you can get an integer (if \(x\) is one or two). However, if you do \(2 \times \frac{1}{3}\), for example, then you get \(\frac{2}{3}\) which is not an integer and not a number like \(\frac{1}{x}\).
Thus, we need to add these numbers too. Because any integer \(y\) multiplied by \(\frac{1}{x}\) is just \(\frac{y}{x}\), more generally we have any number of the form \(\frac{y}{x}\) where \(x\) and \(y\) are integers. The process of adding in more elements in order to satisfy our initial construction is called constructing the closure with respect to the multiplicative inverses 2.
Under this system, every integer has a multiplicative inverse and these inverses themselves can also be added and multiplied to yield other elements that are also of the same form.
Excellent. We’ve now formed the multiplicative completion of the integers (which are themselves the additive completion of the natural numbers, which are the most elementary infinite set). These are called the rational numbers (\(\mathbb{Q}\)) because they can be written as a ratio of two other numbers.
As a quick note, we have to exclude \(\frac{1}{0}\) because it causes contradictions when we attempt multiplication and addition that we don’t like 3. You can include it, and some people do but you lose some important properties that many want. Either way, the general meaning of the rationals excludes fractions with zero underneath.
Note also that if \(b\) is negative, then you can just negate \(a\). Thus we can just say the rationals are everything of the form \(\frac{a}{b}\) where \(a\) is any integer and \(b\) is a natural number, except 0 (so \(b\) is not negative).
Counting
The natural numbers were just things we invented by desiring to create an infinite set. They have, in and of themselves, no relation to the real world. We have to give them meaning. This is a general property of mathematics. Mathematics is about thoughts. Someone has to make them describe reality 4.
Anyway, what does it mean to count? In other words, what does it mean to say there are three of something?
Well, what happens when you ask a child to count toys in a box? The child will take out each toy, say the next number, and then put the toy own, and then take the next toy 5.
In other words, to say there are three of something, I first take the set of \(Z\), \(SZ\), \(SSZ\) (aka, \(0, 1, 2\)), and I assign them to each of the somethings. If I can do this for all the somethings and the labels are unique, I say that there are three of them. If there is a something leftover or I still have labels left to assign, then I say there are not three of those somethings. Pretty easy. Gosh, why do mathematicians talk so much?
This all makes sense for finitely many things but arithmetic is not finite. It’s the study of infinity. So how do we count infinite things? Well, as we said, there’s no physical source of infinite things, so we’ll just go to concepts. First, let’s count the natural numbers. It’s pretty easy, we just have to label them. So let’s start counting. We’ll label zero with \(Z\), one with \(SZ\), etc. How many will we have when we conceptually end? Well, it couldn’t be a number of the form \(S...Z\) (a natural). It would have to be something else, because if it were a natural, then I’d just ask what you’d label the number \(SS...Z\) and you’ll have to give me a new number! Again, since we’re just doing theory, we just invent a notation and call it \(\infty\). We’re just making shit up at this point.
Anyway, anything that can be counted using the natural numbers is called ‘countable’, because we just like to state the obvious.
Notice that the natural numbers are countable, under this definition, but so are the integers. It’s easy. I can absolutely label each integer with a natural number and never reuse them or run out. This is easy to see. For each integer, it’s either negative (i.e. \(-x\)) or positive (i.e. \(x\)). If positive, then I assign the natural number \(2x\). If negative, I assign the natural number \(2x + 1\). Zero maps to itself.
And vice versa, given a natural number, I can give you back every integer. It’s easy. For any natural, if it’s even, I say that it points to half of itself. If it’s odd, I say it points to the negation of half of its successor number. That is, two points to one since two is even and its half is one. One points to negative one because one is odd, and half its next number (2) is one.
So now every integer is labeled and every natural number selects an integer. Because we can go both ways, we find that the natural numbers are actually equal in size to the integers. A surprising result, since intuitively there seem to be “more” integers than naturals. We think this because the naturals are a subset of the integers, and our intuition tells us from our childhood days that if one thing is a subset of another it must have less things. This is true of all finite sets. But we’re talking about arithmetic, the first step to infinity.
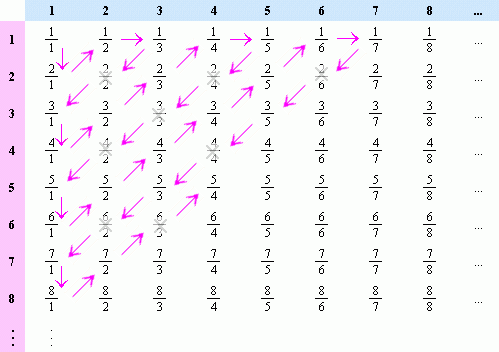
The rationals are also countable, but I’m going to make you stare at a picture to understand it.
Art is never finished, only abandoned
We have now covered the concept of completion and counting. Excellent. We can do all of math now right?
Well, no. I have you reading this blog post so we’re just going to keep beating the horse.
We completed multiplication above, so that means that if we pick one number \(x\) and another number \(z\), we can always find a number \(y\) we can multiply \(x\) by to get \(z\). Above, we chose two numbers \(x\) and \(z\) and found \(y\). Let’s reduce the number of choices. Let’s just pick \(z\) and ask, is there a number \(y\) that when multiplied by itself is \(z\)? Well, let’s just think. If I pick \(z = 2\) then what is \(y\)? Is there any number that when multiplied by itself is 2?
Since \(y\) is a rational number (by definition, since that’s what we’re thinking about), we know it can be written as \(\frac{a}{b}\) for some integer \(a\) and natural number \(b > 0\). Now also note that \(a\) can be either positive or negative because multiplying either by itself yields a positive. This is why your pre-algebra teacher might have writen \(\sqrt(4) = \pm 2\).
Anyway, we have
\[ \frac{a}{b} \cdot \frac{a}{b} = 2 \]
or
\[ \frac{a^2}{ b^{2}} = 2\]
or
\[ a^2 = 2b^2\]
Now we have that \(a^2\) is an even number because it is two multiplied by another number. The product of two odd numbers is odd, so \(a\) must also be even. Thus \(a\) is two multiplied by another number too. Call this number \(m\) and we say \(a = 2m\). Now we have
\[(2m)^2 = 2b^2\]
Or
\[4m^2 = 2b^2\]
\[2m^2 = b^2\]
Oh wow, so \(b^2\) is even too! Using the same reasoning as above, \(b\) is also the product of two with another number \(n\). \(b = 2n\). Great, let’s substitute.
\[\frac{2m}{2n} \cdot \frac{2m}{2n} = 2\]
or
\[\frac{m}{n} \cdot \frac{m}{n} = 2\]
Did you miss it? Again… infinity.
We just picked two numbers that satisfied \(\frac{p}{q} \cdot \frac{p}{q} = 2\) and found that actually there are two smaller numbers \(m\) and \(n\) for which \(\frac{m}{n} \cdot \frac{m}{n}\) is also two. You object, saying we can always find smaller numbers. Absolutely we can… for the rationals. But neither \(m\) nor \(n\) are rationals. They’re an integer and a non-zero natural. We cannot always divide by two. We want infinity, but get nowhere.
You find that there is no least number for \(p\) and \(q\) that satisfy the equation. A real letdown.
Supremum man to the rescue
Well notice that in math we just make things up, so surely we can make up more stuff. Let’s go!
Notice above that we have that \(\frac{3}{2}\) multiplied by itself is \(\frac{9}{4}\) which is greater than two. And also note that \(\frac{4}{3}\) multiplied by itself is \(\frac{16}{9}\) which is less than two. Thus, somewhere in there, the answer must exist, right?
Let’s just find it directly by improving our guess. We’ll start with \(\frac{3}{2}\) and then, since that’s greater than two, decrease our guess a bit. We’ll do this by computing their average.
Let’s start. We take \(\frac{3}{2}\). If we divide \(2\) by this we get \(\frac{4}{3}\). If we had guessed correctly we should have gotten \(\frac{3}{2}\) (the same number). We didn’t so we do it again, but this time we update our guess. Notice that \(\frac{4}{3} \cdot \frac{4}{3}\) is less than 2, so the real answer is somewhere in between \(\frac{3}{2}\) and \(\frac{4}{3}\). To find the number exactly halfway, we take their average.
\[ \frac{1}{2}\left(\frac{3}{2} + \frac{4}{3}\right) = \frac{3}{4} + \frac{4}{6} = \frac{9}{12} + \frac{8}{12} = \frac{17}{12}.\]
Repeat. We find \(2\) divided by \(\frac{17}{12}\) is \(\frac{24}{17}\). Notice that \(\frac{17}{12} > \frac{3}{2}\) (our initial guess) and \(\frac{24}{17} < \frac{4}{3}\) (which was what happened when we divided two by the initial guess). Great, we’re always going to get closer and closer to the real answer here. Eventually, we’ll get it, right?
Well no… infinity. As we showed above (the proof with \(p\) and \(q\)), if you ever get it, you can just get it again, but this time it will be better. If you collect all your guesses and their better values you get an infinite set.
Formalized quickly, to find \(\sqrt{z}\), take a guess \(x_0\) and do the following
\[x_{n + 1} = \frac{1}{2}\left(x_n + \frac{z}{x_n}\right)\].
Quickly, you can verify that for perfect squares, like four, the set of these guesses is finite. That is, they terminate. No infinity. Which is why the square root of perfect squares is easily written.
But all hope is not lost, as we saw above, we can get arbitrarily close to the real answer to \(\sqrt{2}\).
However, the sequence for non-perfect squares will never terminate. That is to say, if our first guess is above the real answer, there will never be a least answer. If there was, just do the procedure outlined above and get a smaller number.
That means there are sets of the rational numbers which have no lower bound in the rational numbers 6.
Again, just as we had to complete the natural numbers when we found addition had no inverse, and we had to complete the integers when we found multiplication had none, we now need to complete the rationals by simply naming a number for each of these sets. We call these numbers the reals (denoted \(\mathbb{R}\)). Note that in my construction above, if I want to “write” down the answer, I can choose any \(x_{n}\) after some sufficiently large \(n\) and say that that number is close enough. If I write out the decimal expansion of these numbers, I get a close “answer” to my problem in finite terms. But note, the decimal expansion has to be infinite because if it weren’t then the set of ever closer answers also ought to be. Again, infinity.
Interestingly enough, these sorts of real numbers also have expansions that do not repeat. They are regular in that they are predictable by computing them using the algorithm above, but they have no repeating pattern. Because of this they’re called irrational.
As a quick note. Just as we had with the rationals where adding a few new numbers required adding many more, we have that here too. If we add \(\sqrt{2}\) as whatever monstrosity we defined above, then we need to add \(\sqrt{2} + \sqrt{3}\) as well. For the sake of not having to write a full book on real analysis, I’m going to ignore how to think about numbers like that, but we’ll need to add them to our set to complete addition and multiplication. More generally, the reals are all rationals plus whatever we want to call the least number in any arbitrarily defined subset of the rationals. I think that sounds a lot more pretentious than it is.
Counting Stars
So we have that the reals are the rationals plus whatever we want to call the ‘least value’ of any arbitrary subset of the rationals. I think it’s reasonable to ask if we can label every real.
Since I’m not really that clever, I’m just going to assume I have a clever oracle that can tell me, for any natural number I give it, a real number in response.
I’m now going to assemble these number into a table, where each row corresponds to the response I get when asking about that row’s number. Note that there are infinitely many columns here. Also note that we’re writing out the decimal expansion, which is fine, since the decimal expansion always converges 7. Moreover, to avoid dealing with the decimal point, the very first column is the position of the decimal in that number. That is for ‘35.55555…’ we have \(2\) in the first column (because there are two digits before the decimal), then \(3\) in the second (first digit) and then \(5\) in the remaining infinite columns.
Now, let’s make a new number, for the \(i\)th row, I’ll make the new number by taking the number in the \(i\)th column and choosing something else randomly. This is illustrated below.
So now I have a new number whose representation in this table is given as above. This number is another real number. I’ve told you how to compute it if you have my special oracle.
Does this number exist on the table?
Again… infinity. The answer is a resounding no. If the number did exist at row \(i\) then the digit at column \(i\) would have to be different from the entry in thet able in row \(i\) (by construction). Thus it cannot occupy any row \(i\).
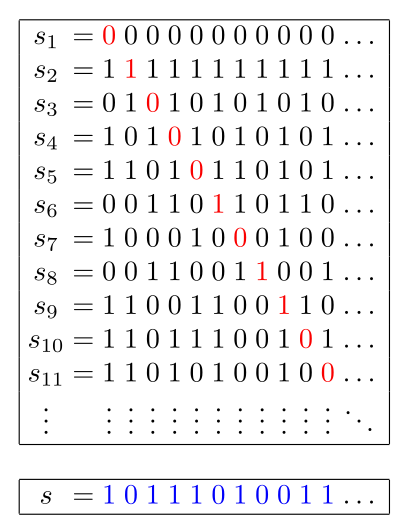
An example of a diagonal argument similar to the one I made above. This shows the argument in base two. All numbers are part of the table, but the number \(s\) cannot be. This is because it requires an \(\infty\) number of columns to represent each real number.
It’s Aleph!
Don’t worry we can always make up new shit. Remember, this is math.
Mathematicians call the size of things like the natural numbers numbers \(\aleph_0\). That funny N thing is the Hebrew letter Aleph. It is pronounced “Aleph-null”.
The size of the real numbers is \(2^{\aleph_0}\). As an exercise to the reader: consider why this is true. First, take a finite set like \({0, 1, 2}\). How many ways are there to form subsets of this set with 3 elements? Then, how many ways are there to form subsets of a set with \(\aleph_0\) elements?.
Some more topics of interest.
There are infinities larger than \(\aleph_0\)! \(\aleph_1\), \(\aleph_2\), etc
You can make \(2^{\aleph_0}\) equivalent to \(\aleph_1\). That is you can just assume that and math works. However, there’s no way of “knowing” whether or not this is true. If you believe, it’s taken axiomatically. It’s not possible to prove it.
You can also assume that \(2^{\aleph_0}\) is not equal to \(\aleph_1\).
That is to say, there are valid proofs using valid logic that the size of the reals is \(\aleph_1\) and that the size of the reals is not \(\aleph_1\). What this means is left up to the reader. This is called the continuum hypothesis. Hopefully this doesn’t lead you to question the very foundation of mathematics and infinity.
The set of all infinities of this sort are called the ‘cardinal’ numbers:
\[\{0,1,2,\ldots,\aleph_0, \aleph_1, \ldots\}\]
This is a ‘transfinite’ set because it includes infinity.
You can do most of math on the cardinal numbers. That is, you can multiply, add, subtract, exponentiate various infinities.
You can go beyond this. If you take the set of all \(\aleph\) numbers and ask what’s the largest of these you have to invent an even larger infinity \(\aleph_\omega\).
There are uncountably many infinities.
Conclusion
Hopefully, this post convinced you that infinity is a lot more complicated than it seemed. While it may seem very easy to come up with an infinite set, the moment we try to think about it in very reasonable ways, we end up with very complicated objects.
This field of counting things is called “discrete mathematics”, and is unfortunately completely ignored by most high school level mathematics courses. It’s unfortunate because it ultimately puts forth several very important questions about the nature of knowledge itself.
In following posts, we’re going to talk about why computation as an abstract principle is innately tied to our knowledge of the real numbers, and knowledge in general.
substitute Z for 0 and S for “1 +”, or count the number of S’s to get the corresponding number.↩︎
Usually closure under some operation means that no matter what inputs you put into the operation, you will get outputs within the same set of things as the input.↩︎
To delve deeper, this is because multiplication distributes over addition and zero is the identity for addition. We have \(x \times (y + 0) = x \times y + x \times 0\) by the distributive property. And we have that \(x \times (y + 0) = x \times y\) by the identity of addition. Thus we have that \(x \times y + x \times 0 = x \times y\), which means that \(x \times 0 = 0\) (recall that zero is the unique identity for addition and the equation above is an identity over addition). This holds true for any operation that acts like multiplication, not just multiplication of natural numbers. “Multiplication” by the additive inverse must yield the additive inverse only. Anyway, now multiplication by the additive identity is not invertible, since every number multiplied by it yields zero. Information is thus lost.↩︎
some disagree.↩︎
if you’re children are anything like mine, they’ll have to do this a few times before they get it right, and might never end if the toys are fun. Theoretically, this process will end.↩︎
do the integers have this property? Think about it↩︎
not going to explain this.↩︎